Logistic Regression
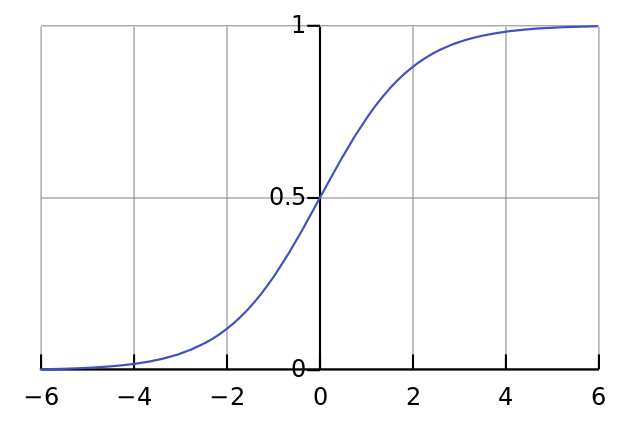
Perhaps you’ve seen some data points and then someone fit a line called the best-fit line to these points; that’s regression.What happens in logistic regression is we have a bunch of data, and with the data we try to build an equation to do classification for us.
Classification with logistic regression and the sigmoid function
理想函数: 接收所有特征,返回预测类别.
对于一个逻辑回归分类器,我们在所有的特征上乘以一个回归系数,求和,带入sigmoid函数,返回一个属于[0,1]的值.任何大于0.5的数据归为1类,小于0.5的归为0类.
$$
\sigma(z)=\frac{1}{1+e^{-z}}
$$
Using optimization to find the best regression coefficients
梯度上升法基本思想:要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻.
对于函数f(x,y),其梯度可以表示为:
$$
\nabla f(x,y)=\begin{pmatrix}\frac{\partial f(x,y)}{\partial x}\ \frac{\partial f(x,y)}{\partial y}\end{pmatrix}
$$
迭代公式如下:
$$
w:=w+\alpha \nabla _wf(w)
$$
α称为步长,或者学习率.该公式一直迭代,直到迭代次数达到规定,或者算法误差到达某个范围.
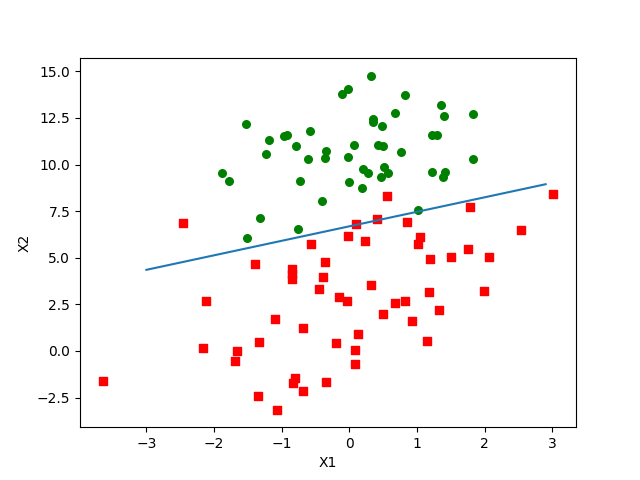
梯度上升算法在每次更新回归系数时,都要遍历整个数据集.如果样本特征和数量很多时,计算复杂度太高.改进策略是,一次只用一个点来更新回归系数,该方法称为随机梯度上升算法.
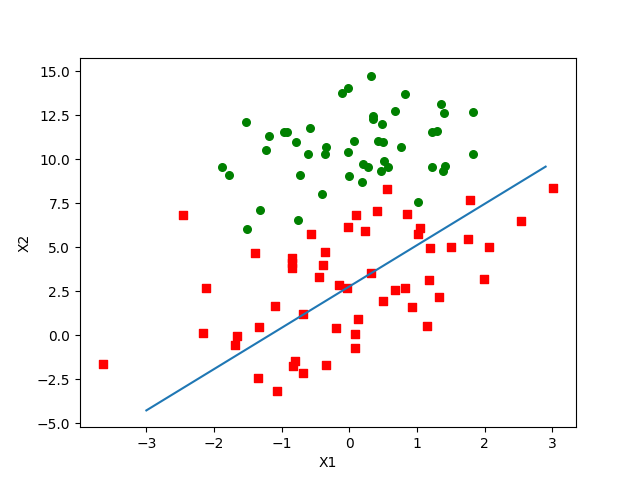
效果更糟了?不不不.当你比较这两种优化算法时,你必须保证得到的回归系数是收敛的.That is, are the parameters reaching a steady value, or are they constantly changing?
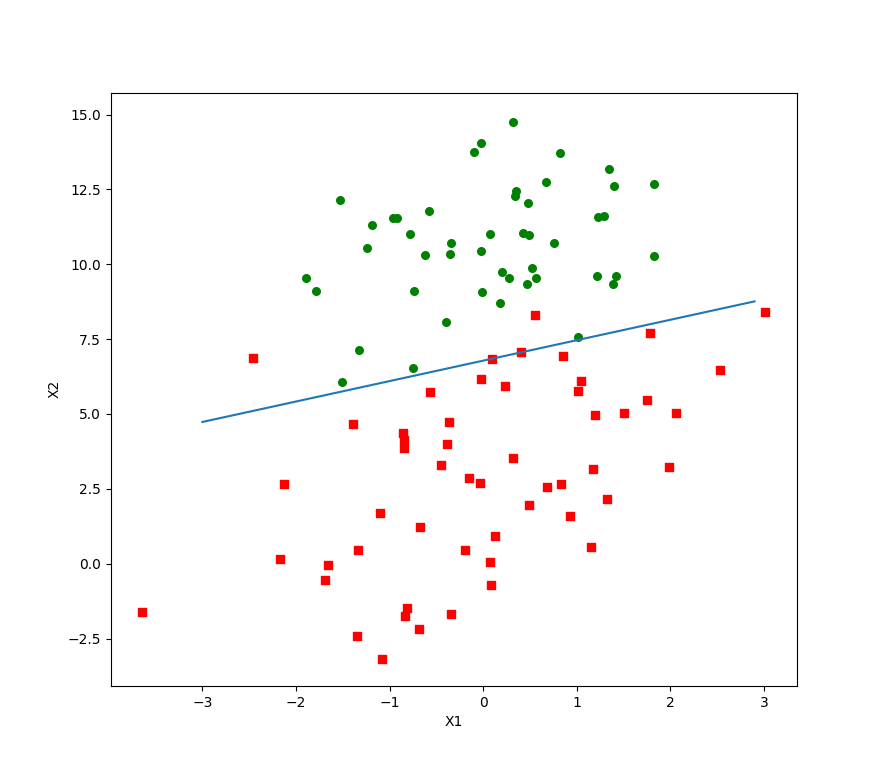
可以看出,效果不错.可如果你有看迭代过程中回归系数的变化情况,会发现一些周期性的波动.样本中不能分类的点(数据集并非线性可分)在每次迭代时都会引发系数的剧烈改变.
我们希望算法能避免来回波动,更快地收敛,于是有了改进的随机梯度上升算法:
1. 步长不再一成不变
2. 随机选取样本更新回归系数,选过的样本丢弃
遍历20次的时候系数基本上就已经收敛了.代码中给的默认迭代次数是150次.
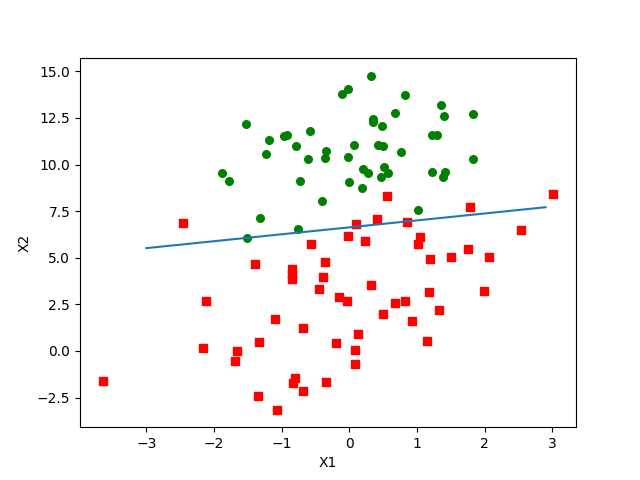
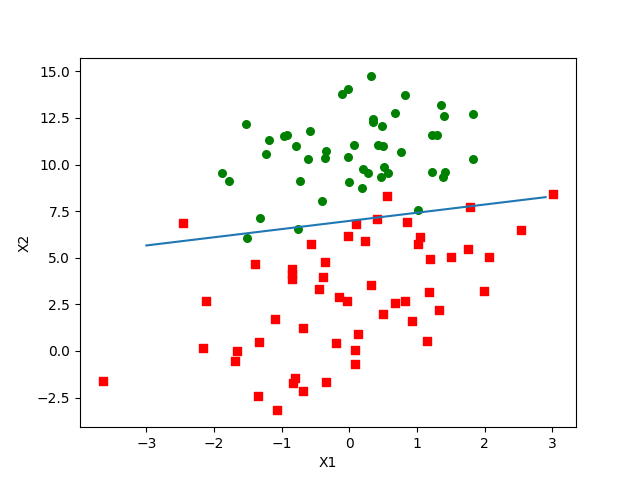
代码链接
https://github.com/yikayiyo/machinelearninginaction/blob/master/Ch05/logRegres.py
Summary
逻辑回归的目的是找非线性函数sigmoid的最佳拟合参数.
为找最佳,最常用的是梯度上升法.
简化版本为随机梯度上升算法,占用更少的计算机资源,是一个在线算法.
通过调整步长和样本选取方式可以继续改进算法.