Task Parallelism

发表于 更新于 本文字数： 1k 阅读时长 ≈ 4 分钟

https://www.coursera.org/learn/parallel-programming-in-java/

Task Creation and Termination (Async, Finish)

以数组求和作为例子

为了求得数组的和，可以将数组分为前后两个部分。两部分的求和可以并行执行，但是在求总和之前要保证两个子任务已经完成。

1
2
3
4
5
finish {
  async SUM1;  // asynchronously compute sum of the lower half of the array
  SUM2;  // compute sum of the upper half of the array in parallel with SUM1
}
SUM;  // combine the two partial sums after both SUM1 and SUM2 have finished

async <stmt1> ：父任务创建子任务执行<stmt1>，并且是并行于父任务的其余部分执行

上面的伪代码中，async SUM1;创建子任务SUM1，和SUM2并行执行

finish <stmt2>：父任务执行<stmt2>，并且等待<stmt2>以及其中创建的异步任务完成

上例中，父任务等待SUM1和SUM2完成，才能执行SUM

Tasks in Java’s Fork/Join Framework

数组求和的分治写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private static class ASum{
  int[] A; // input array
  int LO, HI; // subrange
  int SUM; // return value
  ASum(int[] array, int low, int high){
    this.A = array;
    this.LO = low;
    this.HI = high;
  }
  protected void compute() {
    if (LO==HI) SUM = A[LO];
    else if(LO>HI) SUM = 0;
    else {
      int MID = (LO+HI)/2;
      L = new ASum(A, LO, MID);
      R = new ASum(A, MID, HI);
      L.compute();
      R.compute();
      SUM = L.SUM + R.SUM;
    }
  } // compute()
}

并行写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import java.util.concurrent.ForkJoinPool;
import java.util.concurrent.RecursiveTask;

class ASum extends RecursiveTask<Integer> {  //没有返回值的继承RecursiveAction，比如对数组排序
    final int seqThreshold = 3;
    int[] array;
    int lo, hi;

    public ASum(int[] array, int low, int high) {
        this.array = array;
        this.lo = low;
        this.hi = high;
    }

    @Override
    protected Integer compute() {
        int res = 0;
        if ((hi - lo) <= seqThreshold) {  //不再切分为子任务
            for (int i = lo; i < hi; i++)
                res += array[i];
        } else {
            int mid = (lo + hi) / 2;
            ASum L = new ASum(array, lo, mid);
            ASum R = new ASum(array, mid, hi);
            // L.fork();
            // R.fork();
            invokeAll(L, R);  //和上面的两句等价
            res += L.join() + R.join();
        }
        return res;
    }

    static int sumOfInts(ForkJoinPool pool, int[] array) {
        int n = array.length;
        ASum a = new ASum(array, 0, n);
        return pool.invoke(a);
    }

    public static void main(final String[] args) {
        int[] nums = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
        ForkJoinPool pool = new ForkJoinPool();
        System.out.println(sumOfInts(pool, nums));
    }
    
}

Computation Graphs, Work, Span

Computation Graphs

Computation Graphs (CGs) model the execution of a parallel program as a partially ordered set.

A CG consist of:

  • A set of vertices or nodes, in which each node represents a step consisting of an arbitrary sequential computation.
  • A set of directed edges that represent ordering constraints among steps.

对于fork-join框架，可以将这些有向边分为三类：

  • Continue edges，连接任务中顺序执行的步骤
  • Fork edges，将fork操作连接到子任务的第一个步骤
  • join edges connect the last step of a task to all join operations on that task

一个小例子

1
2
3
4
5
6
S1
fork S2
S3
join S2  // 这里join S2发生在S4之前
S4
// S5 如果有的话，连接到S4之后

对应的CG为

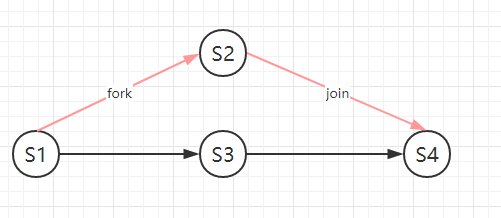
CGs上的data race

没有边连接的两个节点同时写或者读写相同的位置时发生data race

CGs上的理想并行程度 （ideal parallelism）

与计算机的实际并行性无关
$$
ideal,parallelism = \frac{WORK(G)}{SPAN(G)} \tag{1}
$$

其中：

  • WORK(G)为G中所有节点执行时间之和
  • SPAN(G)为G中关键路径上节点的执行时间之和，上例中SPAN(G)为 max((S1,S3,S4), (S1,S2,S4))

Multiprocessor Scheduling, Parallel Speedup

假设

有P个处理器，每个处理器都相同，每一个节点的执行时间都是固定的（不管在那个处理器上），处理器都是贪心地执行任务
T_p表示在p个处理器上执行一个CG所花的时间,
相同的P个处理器，相同的CG，不同的调度算法也可能对应不同的T_p

$$
T_{\infty} \le T_p \le T_1
$$

Speedup(P)

the parallel speedup for a given schedule of a CG on P processors，满足下面：
$$
Speedup(P) = \frac{T_1}{T_P} \tag{2}
$$

$$
Speedup(P) \le P \tag{3}
$$

$$
Speedup(P) \le \frac {WORK}{SPAN} \tag{4}
$$

（3）表示P个处理器不能带来P倍的加速

（4）表示现实骨感，理想丰满

Amdahl’s Law

if q ≤ 1 is the fraction of WORK in a parallel program that must be executed sequentially, then the best speedup that can be obtained for that program for any number of processors, P , is Speedup(P) ≤ 1*/q*.

例如，如果线性工作占比为0.5，则不管处理器个数再多，有Speedup(P) ≤ 2

因为有
$$
WORK(G)*q \leq SPAN(G) \tag{5}\
==> \frac{WORK(G)}{SPAN(G)} \leq \frac{1}{q}
$$
上式表示关键路径用时不小于任务中线性部分的用时