Dynamic programming
发表于
更新于
本文字数:
139
阅读时长 ≈
1 分钟
5 steps to solve DP:
1.subprobs
2.guess
3.recurrence
4.order
5.orig prob
1 | ''' |
决策树
发表于
更新于
本文字数:
289
阅读时长 ≈
1 分钟
构造决策树
第一个问题:当前数据集上哪个特征在划分数据分类时起决定作用?为此需要一个评估标准.
划分的大原则是:将无序的数据变得有序.
划分之后接着划分,递归.
递归结束条件:程序遍历完所有划分数据集的属性或者分支下的数据均为一个类型.
为了度量引入了信息论的东西,也就是熵.
熵
信息的定义:如果待分类的事务可能划分在多个分类中,则符号xi的信息定义为:
$$
l(x_i)=-\log_2 p(x_i),
$$
其中p(xi)是选择该分类的概率.
熵是信息的期望值.我们需要计算所有类别所有可能值包含的信息期望值:
$$
H=-\sum_{i=1}^n p(x_i)\log_2 p(x_i),
$$
其中,n为样本分类.
另外
数据最好是标称型的 ;(对于ID3算法,数值型数据最好是离散的.
出现过拟合时,可以剪枝.
剪枝策略,预剪枝或者后剪枝.
别的决策数算法,C4.5|CART.
https://github.com/yikayiyo/machinelearninginaction/blob/master/Ch03/trees.py
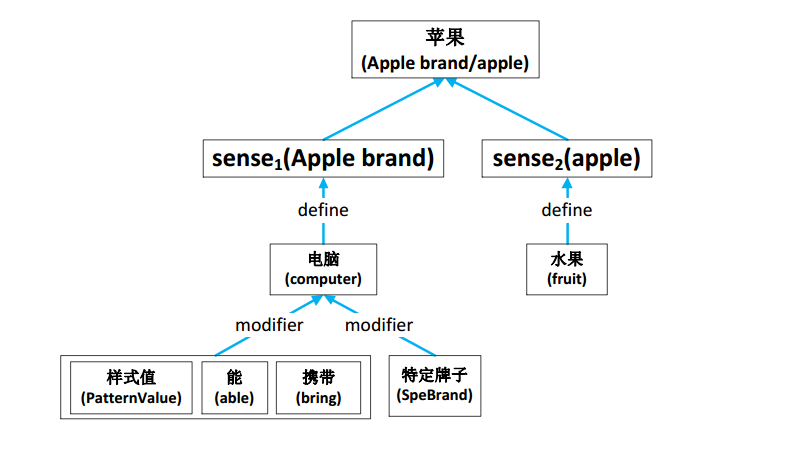
借助义元改善词表示学习
发表于
更新于
本文字数:
1.7k
阅读时长 ≈
6 分钟
简洁的python
发表于
更新于
本文字数:
794
阅读时长 ≈
3 分钟
条件表达式
一般情况下,条件分支只有简单的返回或对同一变量进行赋值操作时,可以转为条件表达式.
1 | #1.改写条件语句 |
列表解析(list comprehension)
将一个列表转为另一个时用更少的代码